퀵 정렬 (Quick Sort)

written by sohyeon, hyemin 💡

1. 퀵 정렬이란?

일반적으로 사용되고 있는 아주 빠른 정렬 알고리즘이다.
정렬 속도가 빠른 데서 착안해 퀵 정렬 이라는 이름이 붙여졌다.
다른 원소와의 비교만으로 정렬을 수행하는 알고리즘이다.

2. 동작 방식

동작을 수행할 때 각 그룹에 대해 pivot설정과 그룹 나눔을 반복하게 되며
모든 그룹이 1명이 되면 정렬을 마치게 된다.

이 과정을 분할정복 (Divide and Conquer)이라고 한다.

1) Divide and Conquer

• Divide (PARTITION과정)

  정렬 해야 할 리스트 안에 있는 한 요소를 선택해 pivot으로 지정,
  pivot을 기준으로 작은 요소들을 왼쪽, 큰 요소들을 오른쪽으로 이동

• Conquer

  pivot을 제외한 왼쪽, 오른쪽 리스트를 다시 정렬
  분할된 부분 리스트에 대해 다시 pivot을 지정하고
  2개의 부분리스트로 나누는 과정 반복

• Pivot 설정

2) 동작 과정

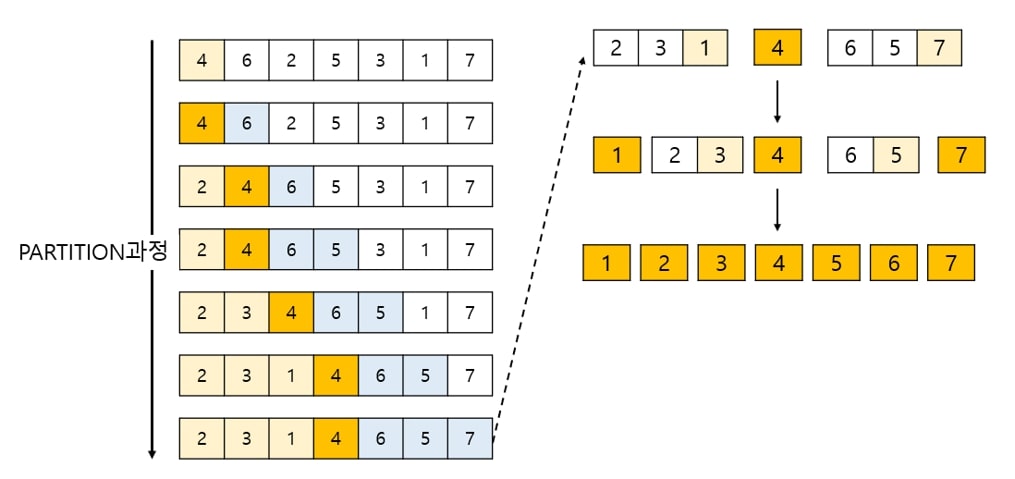
• 임의의 한 요소를 pivot으로 선택
• Pivot을 기준으로 작은 값을 왼쪽, 큰 값을 오른쪽으로 이동
• Pivot을 제외한 왼쪽, 오른쪽 리스트에 partition과정 반복
• 위의 과정을 반복해 각각 분할된 리스트의 크기가 0이나 1이 되면 정렬이 끝남

3. 특징

1) 장점

• 평균적으로 빠른 수행 속도를 가짐

2) 단점

• Unstable한 정렬임

4. 시간 복잡도

입력되는 자료에 따라 시간복잡도가 달라질 수 있다.

1) Worst Case

완전하게 한쪽으로 몰려 그룹이 나뉘는 경우,
left가 n-1개의 요소를 갖고 right가 0개의 요소를 가질 떄

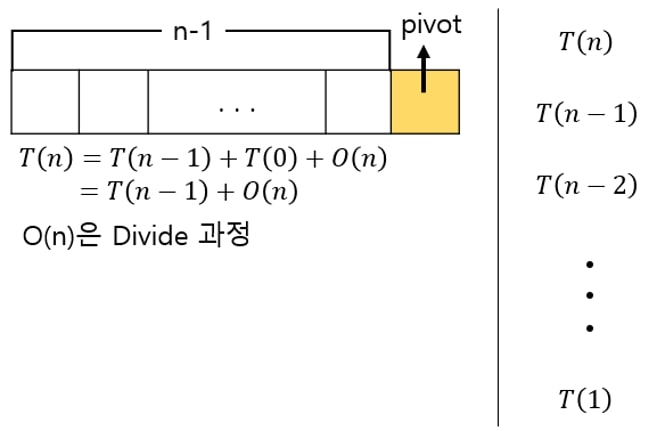
T(n)=1+2+⋯+n-1+n=n(n-1)/2
∴T(n)=O(n^2)

2) Best Case

pivot값이 계속 중앙에 위채해 left, right가 균등하게 나뉠 때

T(n) = 2T(n/2)+O(n) ( O(n)은 Divide과정 )

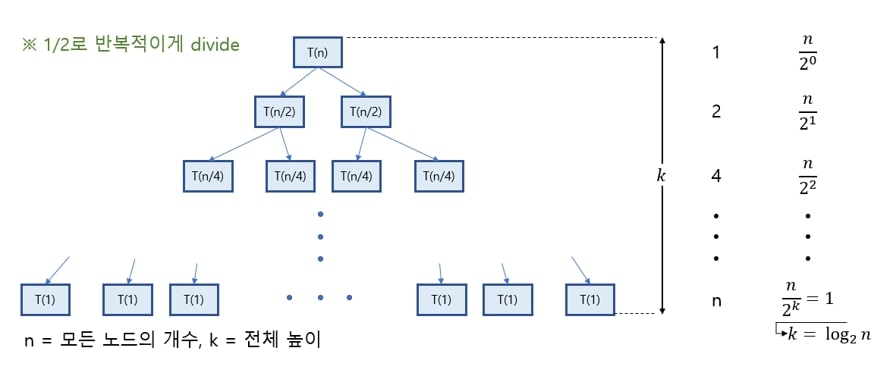
∴T(n)=O(nlog_2⁡n)

3) Average Case

best case에 보통 가까움

• 일정한 비율로 분할 된다면 O(nlog_2⁡n )의 시간 복잡도를 가짐

• 극단적이게 분할되는 비율이 치우친 경우에도 동일함

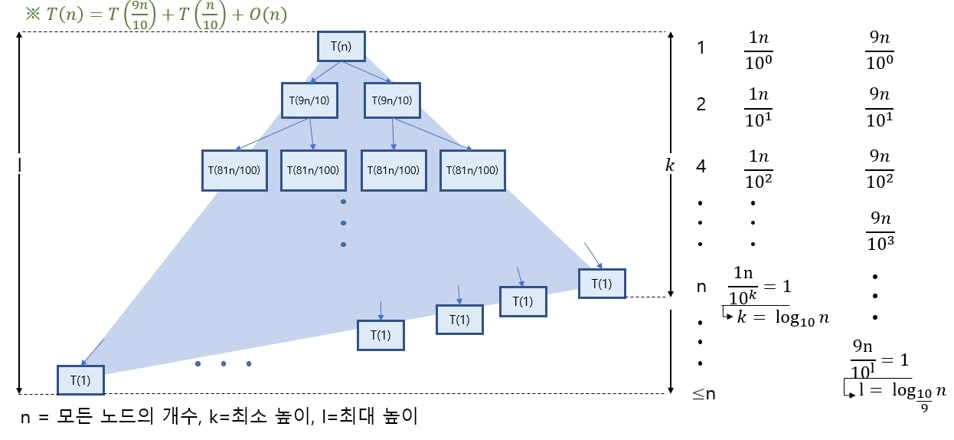
아래 증명에 의해 log_2n으로 표현이 가능하다.

따라서 T(n)은 아래와 같이 구할 수 있다.

4. 예제 코드

import java.util.Scanner;
// 퀵 정렬

class QuickSort {
	// 배열 요소 a[idx1]과 a[idx2]의 값을 바꿉니다.
	static void swap(int[] a, int idx1, int idx2) {
		int t = a[idx1];  a[idx1] = a[idx2];  a[idx2] = t;
	}

	// 퀵 정렬
	static void quickSort(int[] a, int left, int right) {
		int pl = left;					// 왼쪽 커서
		int pr = right;					// 오른쪽 커서
		int x = a[(pl + pr) / 2];		// 피벗

		do {
			while (a[pl] < x) pl++;
			while (a[pr] > x) pr--;
			if (pl <= pr)
				swap(a, pl++, pr--);
		} while (pl <= pr);

		if (left < pr)  quickSort(a, left, pr);
		if (pl < right) quickSort(a, pl, right);
	}

	public static void main(String[] args) {
		Scanner stdIn = new Scanner(System.in);

		System.out.println("퀵 정렬");
		System.out.print("요솟수：");
		int nx = stdIn.nextInt();
		int[] x = new int[nx];

		for (int i = 0; i < nx; i++) {
			System.out.print("x[" + i + "]：");
			x[i] = stdIn.nextInt();
		}

		quickSort(x, 0, nx - 1);			// 배열 x를 퀵 정렬

		System.out.println("오름차순으로 정렬했습니다.");
		for (int i = 0; i < nx; i++)
			System.out.println("x[" + i + "]＝" + x[i]);
	}
}