# 시간복잡도와 Big-O 표기법 (Time Complexity & Big-O)
written by sohyeon, hyemin 💡
# 1. 알고리즘의 분석과 수행시간
# 1-1. 알고리즘의 분석
알고리즘을 실행하는데 필요한 자원을 예측하는 것
메모리, 통신대역, 하드웨어와 같은 자원이 측정의 관심대상이 되기도 하지만
대부분의 경우 측정대상은 계산시간이다.
# 수행시간
기본연산개수 또는 실행된 단계의 횟수
(즉, 알고리즘의 수행시간은 각 명령문 수행시간의 합이다.)
# 알고리즘 수행시간
주어진 문제의 입력크기가 다양하기 때문에
최악, 최상, 평균적인 경우 총 3개의 case를 가질 수 있는데
우리는 최악의 경우에 주로 관심을 둘 것이다.
최악의 경우는 모든 입력에 대한 수행시간의 상한이 되며,
이보다 더 나쁜 경우는 존재하지 않고 최악의 경우가 빈번하기도 함
# 1-2. 시간복잡도
가장 널리 사용되는 알고리즘의 수행시간 기준
알고리즘이 실행되는 동안 수행하는 기본적인 연산의 수를 입력의 크기에 대한 함수로 표현
<시간 복잡도와 입력 크기의 관계>
시간 복잡도가 높다는 것은 입력의 크기가 증가할 때 알고리즘의 수행 시간이 증가한다는 의미이다.
하지만 시간 복잡도가 낮다고 해서 언제나 더 빠르게 동작하는 것은 아니다.
입력의 크기가 작을 때는 시간 복잡도가 높은 알고리즘이 더 빠르게 동작할 수도 있다.
시간 복잡도를 표기하기 쉽게하기 위해 증가차수, 점근적 효율성을 기준으로 알고리즘의 수행시간을 나타낼 것이다.
# 증가차수
더 단순하게 추상화하여 수행시간에 대한 증가비율 또는 증가차수를 이용하는 것
차수가 가장 높은 항만 고려하고 상수 계수는 무시한다.
# 점근적 효율성
입력크기가 극한으로 증가할 때 어떤 알고리즘의 수행시간이 어떻게 증가하는지에 관심을 두고
점근적으로 더 효율적인 알고리즘이 가장 좋은 선택이 되는 것
점근적 표기 방식에 따라,
최상의 경우 : 오메가 표기법 (Big-Ω Notation)
평균의 경우 : 세타 표기법 (Big-θ Notation)
최악의 경우 : 빅오 표기법 (Big-O Notation)
세가지 방식으로 시간복잡도를 나타내는데 사용한다.
이 중에서도 최악의 경우인 빅오를 사용해 최악의 경우를 판단하면 평균과 가까운 성능으로 예측하기 쉽다.
# 2. 빅오 표기법(Big-O Notation)
빅오 표기법은 점근적 상한을 나타내는 것이다.
입력의 크기가 극한으로 증가할때 최고 차항의 차수가 가장 영향을 많이 끼치기 때문에
가장 높은 항을 제외하고 다른 항은 다 제거하는 표기법이다.
즉, 시간복잡도에 가장 큰 영향을 미치는 차항으로 시간복잡도를 나타내는 표기법이다.
T(n)=n^2+2n+9 # O(n2)
T(n)=n^4+n^3+n^2+1 # O(n4)
T(n)=5n^3+3n^2+2n+1 # O(n3)
최고 차항을 제외하고 다 제거하고 계산하기 때문에 계산이 매우 간단하다.
알고리즘의 시간복잡도는 반복문에 의해 결정되므로 반복문이 몇번 실행되는지 보면 된다.
# 예시)
for(int i=0; i<N; i++){
...
for(int k=0; k<N; k++){
...
}
}
위와 같은 경우 N번 수행되는 반복문이 두번 중첩되어있기 때문에 시간복잡도는 O(N^2)이다.
# 2-1. Big-O 표기법의 종류와 성능
# 1) Big-O 표기법의 종류
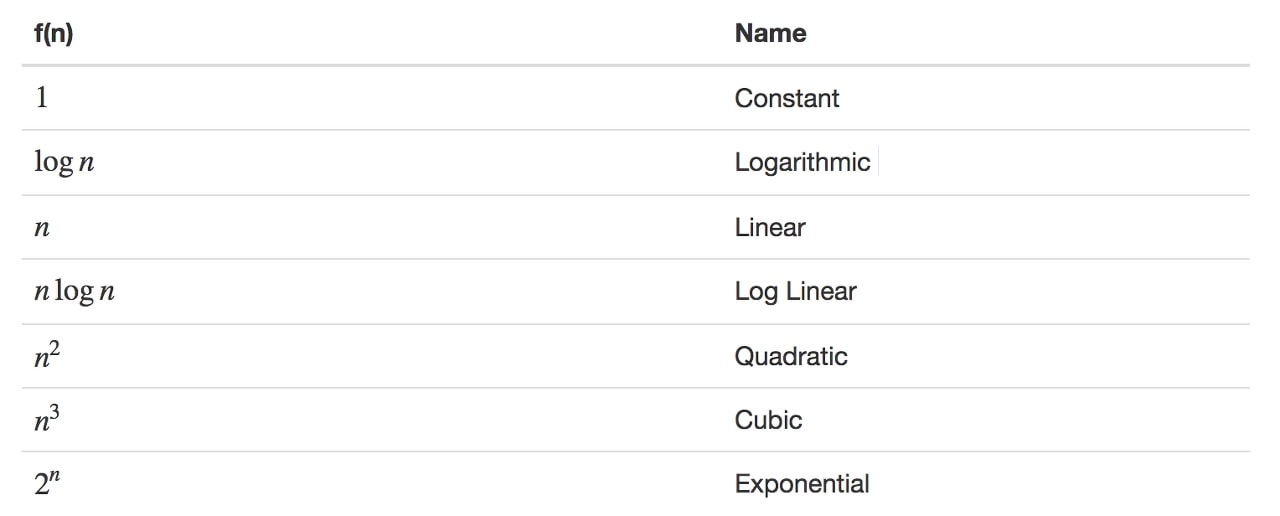
O(1) - (상수) Constant
- 입력되는 데이터양과 상관없이 일정한 실행 시간을 가진다.
- 알고리즘이 문제를 해결하는데 오직 한 단계만 거친다.
O(logN) Logarithmic
데이터양이 많아져도, 시간이 조금씩 늘어난다.
시간에 비례하여, 탐색 가능한 데이터양이 2의 n승이 된다.
문제를 해결하는데 필요한 단계들이 연산마다 특정 요인에 의해 줄어든다.
만약 입력 자료의 수에 따라 실행시간이 이 log N 의 관계를 만족한다면 N이 증가함에 따라 실행시간이 조금씩 늘어난다.
이 유형은 주로 커다란 문제를 일정한 크기를 갖는 작은 문제로 쪼갤때 나타나는 유형이다.
예시: Binary Search
O(N) Linear
- 데이터양에 따라 시간이 정비례한다.
- linear search, for 문을 통한 탐색을 생각하면 되겠다.
O(N log N) log linear
데이터양이 N배 많이 진다면, 실행 시간은 N배 보다 조금더 많아 진다. (정비례 하지 않는다)
이 유형은 커다란 문제를 독립적인 작은 문제로 쪼개어 각각에 대해 독립적으로 해결하고, 나중에 다시 그것들을 하나로 모으는 경우에 나타난다.
N이 두배로 늘어나면 실행 시간은 2배보다 약간 더 많이 늘어난다.
예시: 퀵소트, 머지소트
O(N^2) Quadratic
데이터양에 따라 걸리는 시간은 제곱에 비례한다. (효율이 좋지 않음, 사용하면 안된다)
이 유형은 이중루프내에서 입력 자료를 처리 하는 경우에 나타난다.
N값이 큰값이 되면 실행 시간은 감당하지 못할 정도로 커지게 된다.
문제를 해결하기 위한 단계의 수는 입력값 n의 제곱
예시: 2중 for 문을 사용하는 버블소트, 삽입정렬(insertion sort)
# 2) 성능비교
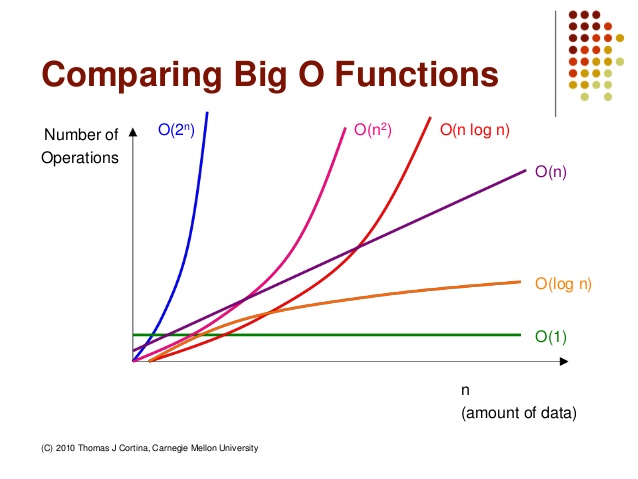
성능 순서 : O(1)<O(logn)<O(n)<O(nlogn)<O(n2)<O(n3)<O(2n)