재귀 알고리즘 (Recursive Algorithm)

written by sohyeon, hyemin 💡

1. 재귀란?

재귀는 자신을 정의할 때 자기 자신을 재참조하는 방법을 말한다.

어떤 사건이 자기 자신을 포함하고 다시 자기 자신을 사용하여 정의될 때 재귀적(recursive)이라고 한다.

재귀 알고리즘에 알맞은 경우는 '풀어야 할 문제', '계산할 메서드', '처리할 데이터 구조'가 재귀로 정의되는 경우이다.

2. 재귀 알고리즘의 활용

1) 팩토리얼

재귀를 사용해 작성할 수 있는 가장 익숙한 예시는 팩토리얼을 구하는 프로그램이다.

1. 0!=1
2. n>0이면, n! = n x (n-1)!

예제 코드

class Factorial{
    static int factorial(int n){
        if(n>0)
            return n*factorial(n-1);
        else
            return 1;
    }
}

2) 유클리드 호제법

두 정수의 최대공약수를 재귀적으로 구하는 방법이다.

22와 8의 최대공약수를 구하는 과정 예시

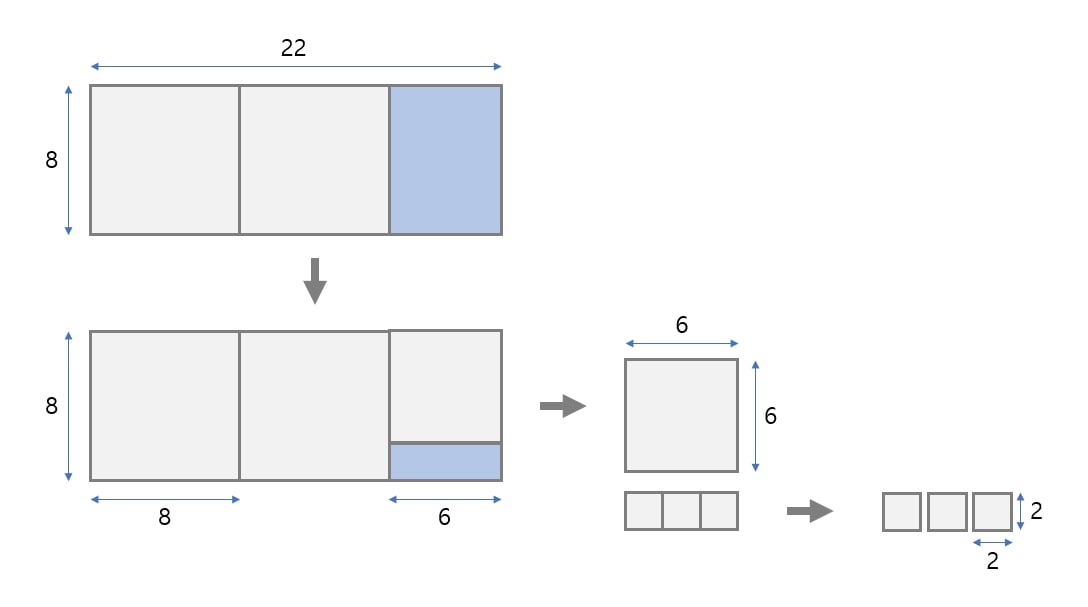
1. 두 정수를 두 변의 길이로 하는 직사각형을 만든다.
2. 직사각형을 정사각형으로 완전히 채운다.
3. 정사각형만으로 채워지지 않을 때, 남은 직사각형에 같은 작업을 반복한다.
4. 정사각형만으로 구성되었을 때의 변의 길이가 최대 공약수이다.

큰 값을 작은 값으로 나눌 때 나누어 떨어지는 가장 작은 값이 최대공약수이다.
나누어지지 않으면 작은값에 대해 나누어 떨어질때까지 같은 과정을 반복한다.

알고리즘

두 정수 x, y의 최대공약수 -> gcd(x, y)

x = az
y = bz
z = gcd(x,y)

y가 0이면 x이고 y가 0이 아니면 gcd(y, x%y)

예제 코드

class EuclidGCD{
    static int gcd(int x, int y){
        if(y==0)
            return 0;
        else
            return gcd(y, x%y);
    }
}

3) 하노이의 탑

작은 원반이 위, 큰 원반이 아래에 위치할 수 있도록 원반을 3개의 기둥 사이에서 옮기는 문제이다.
모든 원반의 크기가 다르고 모든 원반이 이 규칙에 맞게 첫 번째 기둥에 쌓여있다.
모든 원반을 세 번째 기둥으로 최소의 횟수로 옮긴다.
원반은 1개씩 옮길 수 있다.

동작 원리

원반이 n개 존재하고 기둥 3개를 각각 시작 기둥, 중간 기둥, 목표 기둥이라고 할 때 가장 큰 원반을 목표 기둥으로 최소의 이동횟수로 움직이기 위해서는 먼저 가장 큰 원반을 제외한 n-1개의 원반 그룹을 중간 기둥으로 이동시켜야 한다.

이 과정을 크게 3단계로 볼 수 있다.

1. 그룹을 중간 기둥으로 이동
2. 가장 큰 원반을 목표 기둥으로 이동
3. 그룹을 목표 기둥으로 이동

예제 코드

• move(no) : 이동 메서드, 매개변수 no는 옮겨야 할 원반의 개수

• x : 시작 기둥의 번호

• y : 목표 기둥의 번호

  기둥 번호를 1, 2, 3으로 나타냄, 기둥 번호의 의 합이 6이므로
  시작 기둥과 목표 기둥이 무엇이던 중간기둥은 6-x-y로 구할 수 있다.

import java.util.Scanner;

class Hanoi {
	// no개의 원반을 x번 기둥에서 y번 기둥으로 옮김
	static void move(int no, int x, int y) {
		if (no > 1)
			move(no - 1, x, 6 - x - y);

		System.out.println("원반[" + no + "]을 " + x + "기둥에서 " + y + "기둥으로 옮김");

		if (no > 1)
			move(no - 1, 6 - x - y, y);
	}

	public static void main(String[] args) {
		Scanner stdIn = new Scanner(System.in);

		System.out.println("하노이의 탑");
		System.out.print("원반 개수：");
		int n = stdIn.nextInt();

		move(n, 1, 3);	// 1번 기둥의 n개를 3번 기둥으로 옮김
	}
}